Discrete Distributions
The binomial distribution is used when there are exactly two mutually exclusive outcomes of a trial. These outcomes are appropriately labeled "success" and "failure".
The binomial distribution is used to obtain the probability of observing x successes in N trials, with the probability of success on a single trial denoted by p and the probability of getting a failure outcome denoted by q. (q = 1 – p).
The binomial distribution assumes that p is fixed for all trials.
The word binomial indicates that on any single trial of a binomial experiment, only two possible outcomes are possible. These outcomes are labeled success or failure.
Some assumptions are made when using Binomial Distributions:
- The experiment has N identical trials
- Each trial has only two possible outcomes, labeled as success or failure.
- Each trial is independent of the previous trials.
- The terms p and q remain constant throughout the experiment, where p is the probability of getting a success and q is the probability of getting a failure on any one trial.
The binomial distribution is probably the most commonly used discrete distribution.
The binomial formula is:
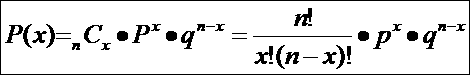 |
Where:
n = the number of trials (or the number being sampled)
x = the number of successes desired
p = the probability of getting a success in one trial
q = 1 – p = the probability of getting a failure in one trial
We will review three types of discrete distributions:
- binomial distributions
- Poisson distribution
- hypergeometric distribution
